点とベクトルと座標変換

はじめに

研究室で座標変換について説明する機会が何回かありました．本記事ではそこで説明した内容をまとめます．

本記事ではまず，「点」と「ベクトル」を定義します．次に，「座標」と「座標系」を定義します．そして，行列を用いた座標変換について解説します．

点とベクトル

定義

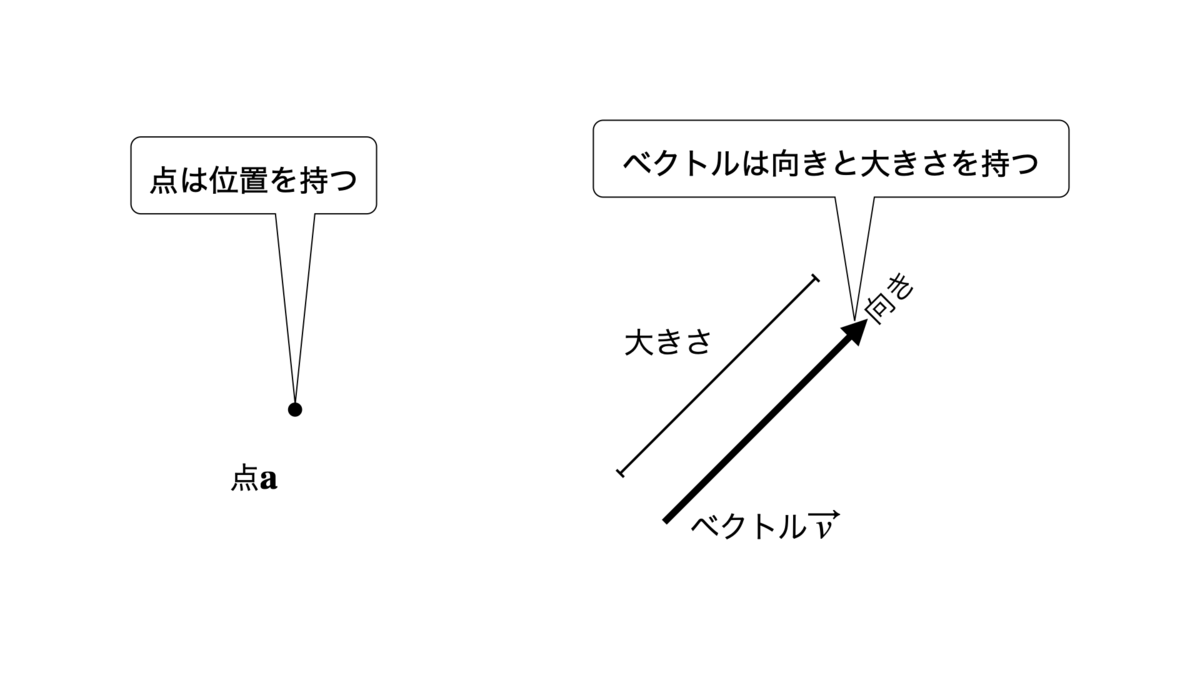
点とは位置を持つものです．以下では点を太字の文字（例えば， $𝐚$ ）で表すことにします．

ベクトルとは向きと大きさをものです．以下ではベクトルを矢印のついた文字（例えば， $\vec{v}$ ）で表すことにします．

以下に点とベクトルの例を示します．

演算

ベクトルの実数倍

ベクトル $\vec{v}$ の実数 $k$ 倍 $k \vec{v}$ は次のようなベクトルを表します．

$k > 0$ の場合： $\vec{v}$ と同じ向きで大きさを $| k |$ 倍にしたベクトル
$k < 0$ の場合： $\vec{v}$ と逆の向きで大きさを $| k |$ 倍にしたベクトル
$k = 0$ の場合：大きさが $0$ のベクトル

ベクトルの和

ベクトル $\vec{u}$ とベクトル $\vec{v}$ の和 $\vec{u} + \vec{v}$ は次のようなベクトルを表します．

$\vec{u}$ の終点と $\vec{v}$ の始点を一致させるように $\vec{u}$ ， $\vec{v}$ を平行移動させたときに， $\vec{u}$ の始点から $\vec{v}$ の終点へ向かうベクトル

点の平行移動

点 $𝐚$ のベクトル $\vec{v}$ による平行移動 $𝐚 + \vec{v}$ は次のような点を表します．

$𝐚$ から $\vec{v}$ の方向に $\vec{v}$ の大きさの分だけ移動した先の点

以下に点とベクトルの演算の例を示します．

座標と座標系

点の位置を数値を用いて表現することを考えます．座標系とは点の位置を数値を用いて表現するときに基準となるものです．座標系は一つの点といくつかのベクトルで構成されます．座標系を構成する点は原点を，ベクトルは座標軸を表します．ある点の座標とはその点の位置を表現する数値の組です．

具体的には，点 $𝐨$ とベクトル $\vec{v_{0}}$ ， $\vec{v_{1}}$ で構成された座標系を $(𝐨, \vec{v_{0}}, \vec{v_{1}})$ とし，ある点 $𝐚$ が $𝐨$ ， $\vec{v_{0}}$ ， $\vec{v_{1}}$ と実数 $a_{0}$ ， $a_{1}$ を用いて $𝐚 = 𝐨 + a_{0} \vec{v_{0}} + a_{1} \vec{v_{1}}$ と表せる時，座標系 $(𝐨, \vec{v_{0}}, \vec{v_{1}})$ を基準とした点 $𝐚$ の座標は $(a_{0}, a_{1})$ となります．

以下に座標系と座標の例を示します．

座標変換と座標変換行列

座標変換とは，ある座標系を基準とした点の座標を，別の座標系を基準とした座標として表現し直すことです．ここでは，行列を用いて座標変換を行う方法と，逆に座標変換前後の座標から座標変換で用いられた行列を求める方法を解説します．

行列を用いて座標変換を行う

以下の点と行列が与えられたとします．

点 $𝐚$ ：座標系 $(𝐨, \vec{v_{0}}, \vec{v_{1}})$ を基準とした座標が $(a_{0}, a_{1})$ である．
行列 $M$ ： $M = (\begin{matrix} m_{00} & m_{01} & m_{02} \\ m_{10} & m_{11} & m_{12} \\ 0 & 0 & 1 \end{matrix})$

この時， $\begin{matrix} 𝐩 & = 𝐨 + m_{02} \vec{v_{0}} + m_{12} \vec{v_{1}} ， \\ \vec{u_{0}} & = (m_{00} + m_{02}) \vec{v_{0}} + (m_{10} + m_{12}) \vec{v_{1}} ， \\ \vec{u_{1}} & = (m_{01} + m_{02}) \vec{v_{0}} + (m_{11} + m_{02}) \vec{v_{1}} \end{matrix}$ を満たす別の座標系 $(𝐩, \vec{u_{0}}, \vec{u_{1}})$ を考え，その座標系を基準とした点 $𝐚$ の座標 $(b_{0}, b_{1})$ を次のように求めることができます． $\begin{matrix} (\begin{matrix} b_{0} \\ b_{1} \\ 1 \end{matrix}) & = & M (\begin{matrix} a_{0} \\ a_{1} \\ 1 \end{matrix}) \\ = & (\begin{matrix} m_{00} & m_{01} & m_{02} \\ m_{10} & m_{11} & m_{12} \\ 0 & 0 & 1 \end{matrix}) (\begin{matrix} a_{0} \\ a_{1} \\ 1 \end{matrix}) \\ = & (\begin{matrix} m_{00} a_{0} & + & m_{01} a_{1} & + & m_{02} \\ m_{10} a_{0} & + & m_{11} a_{1} & + & m_{12} \\ 1 \end{matrix}) \end{matrix}$

座標変換で用いられる行列を座標変換行列と呼びます．

以下に行列を用いて座標変換を行う例を示します．

座標変換行列を求める

ある2つの座標系 $(𝐨, \vec{v_{0}}, \vec{v_{1}})$ ， $(𝐩, \vec{u_{0}}, \vec{u_{1}})$ と以下の3点が与えられたとします．

点 $𝐚_{0}$ ：
座標系 $(𝐨, \vec{v_{0}}, \vec{v_{1}})$ を基準とした座標： $(a_{00}, a_{10})$
座標系 $(𝐩, \vec{u_{0}}, \vec{u_{1}})$ を基準とした座標： $(b_{00}, b_{10})$
点 $𝐚_{1}$ ：
座標系 $(𝐨, \vec{v_{0}}, \vec{v_{1}})$ を基準とした座標： $(a_{01}, a_{11})$
座標系 $(𝐩, \vec{u_{0}}, \vec{u_{1}})$ を基準とした座標： $(b_{01}, b_{11})$
点 $𝐚_{2}$ ：
座標系 $(𝐨, \vec{v_{0}}, \vec{v_{1}})$ を基準とした座標： $(a_{02}, a_{12})$
座標系 $(𝐩, \vec{u_{0}}, \vec{u_{1}})$ を基準とした座標： $(b_{02}, b_{12})$

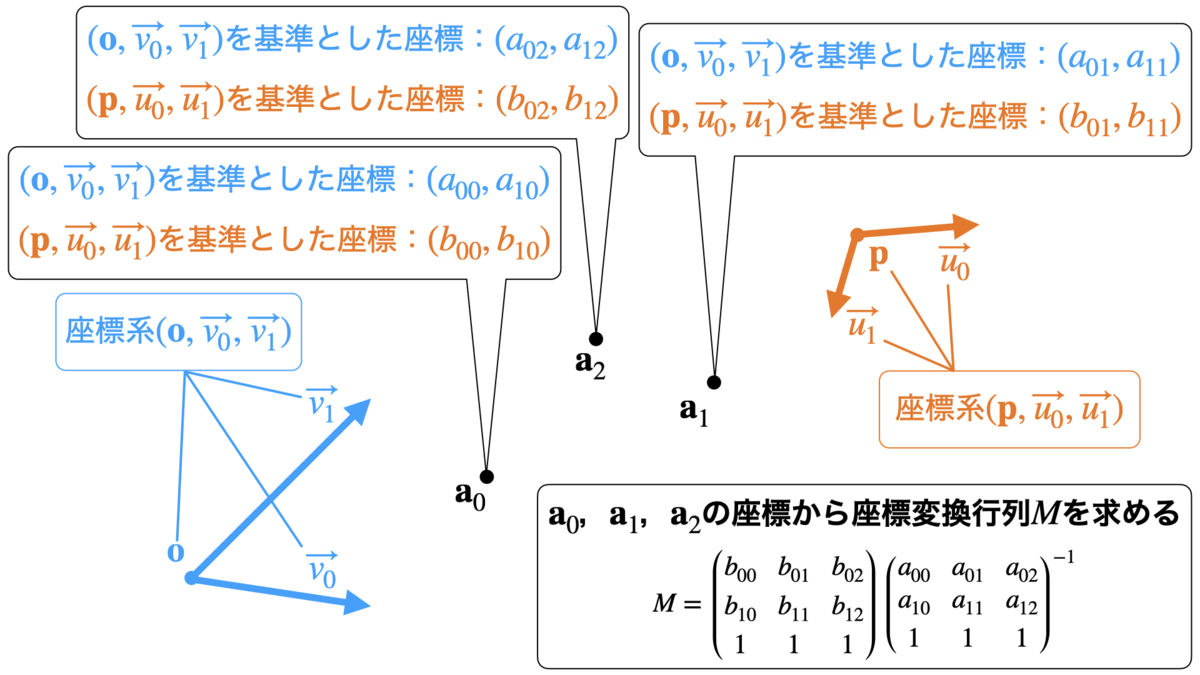
この時，座標系 $(𝐨, \vec{v_{0}}, \vec{v_{1}})$ を基準とした任意の点の座標を，座標系 $(𝐩, \vec{u_{0}}, \vec{u_{1}})$ を基準とした座標に変換する座標変換行列 $M$ を次のように求めることができます．

まず， $𝐚_{0}$ ， $𝐚_{1}$ ， $𝐚_{2}$ を行列 $M$ を用いてそれぞれ座標変換すると $𝐛_{0}$ ， $𝐛_{1}$ ， $𝐛_{2}$ となることから， $(\begin{matrix} b_{00} \\ b_{10} \\ 1 \end{matrix}) = M (\begin{matrix} a_{00} \\ a_{10} \\ 1 \end{matrix})$ ， $(\begin{matrix} b_{01} \\ b_{11} \\ 1 \end{matrix}) = M (\begin{matrix} a_{01} \\ a_{11} \\ 1 \end{matrix})$ ， $(\begin{matrix} b_{02} \\ b_{12} \\ 1 \end{matrix}) = M (\begin{matrix} a_{02} \\ a_{12} \\ 1 \end{matrix})$ が成り立つはずです．これらをまとめて $(\begin{matrix} b_{00} & b_{01} & b_{02} \\ b_{10} & b_{11} & b_{12} \\ 1 & 1 & 1 \end{matrix}) = M (\begin{matrix} a_{00} & a_{01} & a_{02} \\ a_{10} & a_{11} & a_{12} \\ 1 & 1 & 1 \end{matrix})$ と表すことができ，以下のように $M$ について解くことで座標変換行列を求めることができます． $M = (\begin{matrix} b_{00} & b_{01} & b_{02} \\ b_{10} & b_{11} & b_{12} \\ 1 & 1 & 1 \end{matrix}) {(\begin{matrix} a_{00} & a_{01} & a_{02} \\ a_{10} & a_{11} & a_{12} \\ 1 & 1 & 1 \end{matrix})}^{- 1}$

以下に座標変換行列を求める例を示します．

まとめ

まず，「点」，「ベクトル」，「座標系」，「座標」を定義した．
座標変換行列を用いて点を座標変換する方法について解説した．
座標変換前後の点の座標から座標変換行列を求める方法について解説した．
数式はMathMLで書いた．